Problem
A function 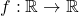 is called even if
is called even if
![Rendered by QuickLaTeX.com \[ f(-x) = f(x)\]](https://www.risanp.com/notes/wp-content/ql-cache/quicklatex.com-d4d24fc5bf4e70df11bb08e30111f732_l3.png)
for all
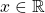
. A function
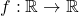
is called odd if
![Rendered by QuickLaTeX.com \[ f(-x) = -f(x)\]](https://www.risanp.com/notes/wp-content/ql-cache/quicklatex.com-bbaabf824635d05026d9a8a357205444_l3.png)
for all
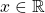
. Let
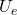
denote the set of real-valued even functions on
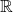
and let
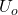
denote the set of real-valued odd functions on
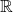
. Show that:
![Rendered by QuickLaTeX.com \[ \mathbb{R}^\mathbb{R}=U_e \oplus U_o\]](https://www.risanp.com/notes/wp-content/ql-cache/quicklatex.com-ec41fd47c1ab9b8c8bf058f09ddb98fd_l3.png)
Proof. To show that
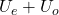
is a direct sum, it is sufficient to prove that
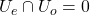
. Let
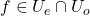
. Hence,
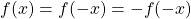
for all
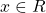
, which only happens for
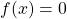
. Hence,
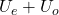
is a direct sum.
Let
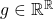
. The equation
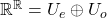
means that
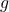
can be written as the sum of an odd function

and an even function

. Or in other words, for all
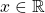
:
(1) 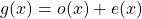
and also:
(2) 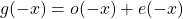
By the definition of the odd and even functions, (
2) can be written as:
(3) 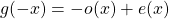
The system of linear equations (
1) and (
3) has a unique solution
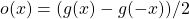
and
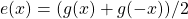
. Hence,
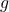
can always be uniquely written as the sum of an odd function and an even function.

![]() is called even if
is called even if![]()
![]()
![]()
![]()
![]()
![]()
